Practical Covariance and Contravariance

For a more in-depth rundown on covariance and contravariance explained in terms of category theory have a look at Thomas Patricek’s blog

Covariance and contravariance are things you’ll probably ignore until you start using generics in ernest. Then one day you’ll want to pass an enumerable to a function that takes a slightly different yet related type of enumerable and then BAM – you’re hit with some crazy error messages and then all of a sudden you’re up to your elbows in browser tabs of StackOverflow articles.

To cut straight to the chase, this is the problem:

Base rawBase = new Derived(); // this works
MyType<Base> wrappedBase = new MyType<Derived>(); // ERROR!

Sometimes we want the OO polymorphism substitution rules (AKA Liskov’s substitution principle) to apply to generic types too. Covariance and contravariance provide us a mechanism to allow this substitution to take place.

To be more specific, [co|contra]variance are necessitated due to the interaction of two different forms of polymorphism – object inheritance and generic typing. And yet sometimes you want to combine the two – while MyType<T> and MyType<U> share no inheritance relationship and therefore are not substitutable for each other, sometimes you want to treat them as if they are substitutable if T and U are themselves related.

So a covariant or contravariant generic type (e.g., a IEnumerable<T>) might be bound to other references of that type (e.g., IEnumerable<U>) when there is an inheritance relationship between the two predicated types. This allows you to pass your IEnumerable<Employee> to a function that actually accepts an IEnumerable<Person> without the compiler complaining that they are different types.

The rule of thumb with inheritance is that if U inherits from T you could say that U is-a-kind-of T. With covariant and contravariant types, I like to think of them in terms of can-be-used-as-a relationship. To determine if MyType should be covariant or contravariant you could ask if Dog is-a-kind-of Animal, is it true that MyType<Dog> can-be-used-as-a MyType<Animal>?

Covariance and contravariance are two different ways that differently specialised generic types should themselves be substitutable for each other like derived types are:

Covariance: MyType<T> is covariant if typing MyType<Base> x = new MyType<Derived>() makes sense (this looks very much like standard substitution rules.)

An example of this is an IEnumerable-derived type, and is classified as having methods that return the predicated type, or getters (hence C# uses the out keyword.)

The implication is that the relationship between the covariant generic types is the same as the relationship between their predicated types, e.g.:

Base b = new Derived(); // OK because of Liskov substitution

IEnumerable<Derived> ds = new List<Derived>();
IEnumerable<Base> bs = ds; // OK because IEnumerable is covariant
Base first = bs.First();

Contravariance: MyType<T> is contravariant if typing MyType<Derived> x = new MyType<Base>() makes sense.

An example of this is the .Net generic Action type, and is classified as having methods that accept the predicated type as a parameter, or setters (hence C# uses the in keyword.)

Contravariant types are probably less common than covariant types, and imply that the relationship between the generic types is the inverse of the relationship between their predicated types. E.g.:

Action<Base> b = _ => {};
Action<Derived> d = b; // OK because Action is contravariant
d.Invoke(new Derived()); // invoke alias 'd', actually invokes 'b'

Why they’re helpful

Covariance and contravariance are useful in all the ways that Liskov’s substitution principle is useful with regular polymorphic types – they are a mechanism that lets you inform the compiler when it’s safe to bind an instance of one generic type to a reference of the same generic type with a different generic parameter.

If you’re writing an application you’ll often have one library or area of your code where you deal with heterogeneous types of one category, lets say Animals, yet in another area of your code you’ll deal exclusively with another related type, lets say Dogs. (Note that in math these are called categories and there is a whole set of theories in how to reason about them. See Thomas Patricek’s blog for more details.)

To be very clear, covariance and contravariance only applies to:

generic types
where the predicated types have an inheritence relationship
where a concrete object of that generic type is being bound to a reference (e.g., a passed as a parameter) of a different specialisation of that type

Liskov substitution without generics

For example as a reminder of the standard substitution rules:

(C#) example of OO substitution rules in action

class Animal {};
class Dog : Animal {};
class Poodle : Dog {};

void SaveDog(Dog dog) { ... }
Dog LoadDog() { ... }

Animal myAnimal = ... ;
SaveDog(myAnimal); // ERROR - myAnimal might be a cat!
Animal myAnimal2 = LoadDog(); // OK - dog is a kind of animal

Poodle myPoodle = ...;
SaveDog(myPoodle); // OK - poodle is a kind of dog
Poodle myPoodle2 = LoadDog(); // ERROR - LoadDog might return a non-poodle dog!

OK cool, this is just how polymorphism works in OO languages. But here’s where it gets confusing – what about generic types that are predicated on those types? E.g., a IEnumerable<Dog> or a Action<Dog>?

Liskov’s substitution of generic types

Covariance and Contravariance hints tell the compiler to allow references to generic types to obey the same rules as polymorphic types! It doesn’t affect how you can use a particular type directly, but it affects what other types of that generic object it can be bound to (when being passed to or returned from functions, for example).

To extend the previous example:

// should be covariant but is not
interface IReader<T> {
  T Read() {...}; // simplified interface
};

// should be contravariant but is not
interface IWriter<T> {
  void Write(T entity); // simplified interface
}

void PrintDogFrom(IReader<Dog> dogReader) {
  Dog dog = dogReader.Read();
  // ... print dog info or something
}

void WriteDogTo(IWriter<Dog> dogWriter) {
  dogWriter.Write(new Poodle());
}

// demonstrating a typical 'reading' usage scenario
// that should work ideally

IReader<Poodle> poodleReader = ...; // init somehow
PrintDogFrom(poodleReader); // ERROR! (IReader<Poodle> != IReader<Dog>)
// BUT it should be OK (poodles are dogs)

// demonstrating a typical 'writing' usage scenario
// that should work ideally

IWriter<Animal> animalWriter = ...; // init somehow
WriteDogTo(animalWriter); // ERROR! (IWriter<Animal> != IWriter<Dog>)
// BUT it should be OK (writer holds animals, can write dogs)

We recognise that a IReader<Poodle> instance should be able to be bound to a IReader<Dog> reference if Poodle is a subclass of Dog. This is known as covariance and is denoted in C# by labeling the generic type with the out keyword:

We can also see that IWriter<Dog> should be able to be bound to IWriter<Animal> if Animal is a superclass of Dog. This is known as contravariance and is denoted in C# by labeling the generic type with the in keyword.

// IReader is covariant on T
interface IReader<out T> {
  ... // as before
}

// IWriter is contravariant on T
interface IWriter<in T> {
  ... // as before
}

The difference in the two interfaces is simple – covariance is used when the dependent type is retrieved out of the generic type (an example would be how an IEnumerable<T> returns objects of type T and therefore is covariant on T). A generic type should be contravariant if it accepts the dependent type as input into its interface (an example would be how an Action<T> takes an instance of T as input when it is run, therefore it is contravariant on T).

Here’s an attempt to visually represent valid type conversions for a cass hierarchy, a representative covariant type (IReader) and a representative contravariant type (IWriter):

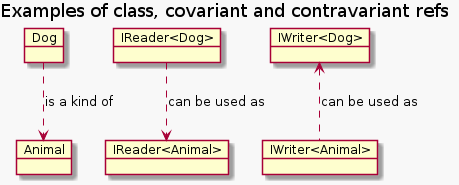
When should my interfaces be covariant or contravariant?

I only add this when its needed, but one thing you’ll find is that you cannot have a covariant or contravariant type if you are both returning and accepting the dependent type in your interface. This is why in C# IEnumerable is covariant but IList is not – because IList allows you to add elements to the collection as well as retrieve the elements in the collection.

Sometimes you will be forced to make your type covariant if you want to use it in certain ways. In this case you may have to separate out the reading part of your interface into a separate interface and have the generic parameter be covariant there only.

A few language-specific quirks you might run across

Although the samples here might suggest otherwise, C# only allows interfaces, not concrete classes, to be specified as covariant or contravariant.

Java never used to support variance specifications much to its detriment. Java arrays behave in a covariant way, but because the interface supports both retrieving and setting elements, the following compiles (or at least used to, I havent tried it recently:)

Dog[] dogs = new Dog[10]; // ...
Animal[] dogsAsAnimals = dogs;
dogsAsAnimals[0] = new Cat(); // whaa?

Note: in researching this I discovered that C# arrays suffer from the same problem! Arrays in both languages will throw runtime exceptions when used illegally like this

C# has supported variance for a long time, but unfortunately there are some corners where they have not yet added it. I recently found out that Task<T> is not covariant, and so if you were implementing your own covariant type, its interface cannot return generic Task<> types, which is frustrating because thats what Microsoft strongly recommend you to do.

Example:

interface IReader<out T> {
  T GetNext();
  Task<T> GetNextAsync(); // compile error! although this should be idiomatic!
}

The official answer to this (well, Jon Skeet’s word is very highly considered) was that adding variance to your interfaces quickly gets complicated in some way and so try to make your types invariant, and I cannot answer to that. My solution was to have the interface return a non-generic Task and dynamically downcast it to the generic type when I used it. This is not great, but its also quite safe as you know for certain the type of the task.

C++ generics (templates) do not directly support the notion of covariance or contravariance, but they don’t need to – templates are specialised at compile time to generate separate instances for each required specialisation, so generic types are often not required to be coerced into other generic types.

For example:

template <typename T>
void printBases(vector<T*> & bases) {
  foreach (auto * b : bases) {
    cout << b->Name() << endl;
  }
}

vector<Derived*> ds {};
printBases(ds); // works as long as Derived has Name() method

template <typename T>
void addDerived(vector<T> & deriveds) {
  deriveds.push_back(new Derived{});
}

vector<Base*> bs {};
addDerived(bs);

The above code shows that C++’s templates are generally sufficient for performing generic operations on generically encapsulated types. The only constraings put on the type passed to the function is that it has a Name() method (this is known as ‘duck-typing’). Note that these are completely type-safe, as the compiler generates fully typed code at compile time. If I tried to add a Base type to a Derived vector, for example, you would get the expected error because the compiler would recognise the type mismatch.

On a related topic, it is also worth noting that C++ allows a derived class’ overridden virtual methods to have covariant return types such that:

struct Base {};
struct Derived : Base {};

struct BaseFactory {
  virtual Base * create() { return new Base{}; }
};

struct DerivedFactory : BaseFactory {
  override Derived * create() { return new Derived{}; }
};

DerivedFactory * ds = new DerivedFactory();
Derived * d = ds->create();

BaseFactory * bs = ds;
Base * b = bs->create();

Java also supports covariant return types, but C# does not.

Seshbot Programs

...and makes software